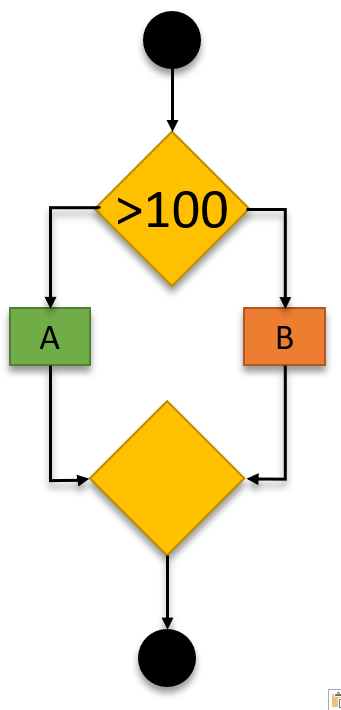
Correct code can still fail
When my code fails, its not always the code that has the failure. Sometimes it can be quirks in the framework, programming language, or even the hardware itself. My code will need to deal with these quirks, for the problem to be fixed. Small values Lets take the following...
Read More