The truth about Truth

Posted On May 11, 2017

Truth can never be an attribute of a single object.

Truth is the relation of similarity between two or more objects.

The problem

My parents, elders, priests and scientists often told me what was true and what was not. But why?

• • Parents: “Because I say so!”

• • Elders: “Because I am more experienced than you.”

• • Priests: “Because it’s God’s will.”

• Scientist: “Because it’s science.”

I guess parents were the most honest about, that they didn’t have a clue.

Euclides postulated, that “the sum of all the inside angles of the triangle is always 180°”. I did understand the correlation, but never understood:

1. 1. Why is it true? (I was told: “because Euclides said so”)

1. 1. Is it true for all the triangles? (I was told: “yes”…)

1. Would it always remain true? (I was told: “yes! … and that I shouldn’t ask this kind of questions.”)

The meaning of “Truth”

I jumped into philosophy to find truth about truth.

• • 1st I found out, that there were a lot of postulates, which were considered true.

• • Then I experienced, that philosophers did disagree which each other.

• Then I discovered the existence of multiple schools of philosophy, which accept some philosophers as “true” and view the others as sophists (liars, manipulators) or just mad ramblers.

But I did find some interesting postulates about truths:

• • The correspondence theory: truth means a belief is true if there exists a fact to which the belief correspond.

• • Realism: truth means a representation of an objective world.

• • Anti-realism: truth means something verifiable.

• Truth Pluralism: truth can be multiple concepts and therefore ambiguous.

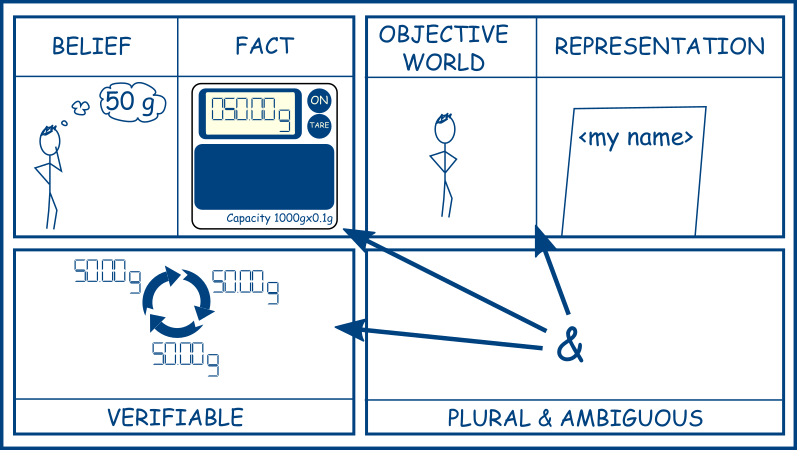
To put it short: truth can be a fact, something objective, something verifiable or something ambiguous.

What about truth in math?

Can something true become untrue? Like 2+2=4?

Let’s get back to Euclidean’s postulate about triangles. If I could find a triangle with the sum of the inside angles other than 180°, then Euclidean’s postulate would become untrue:

• • Riemannian proved that the sum could be greater than 180° when triangles are made on a sphere.

• Lobachevski showed that the sum could be lesser than 180° when triangles are made on a hyperbolic figure.

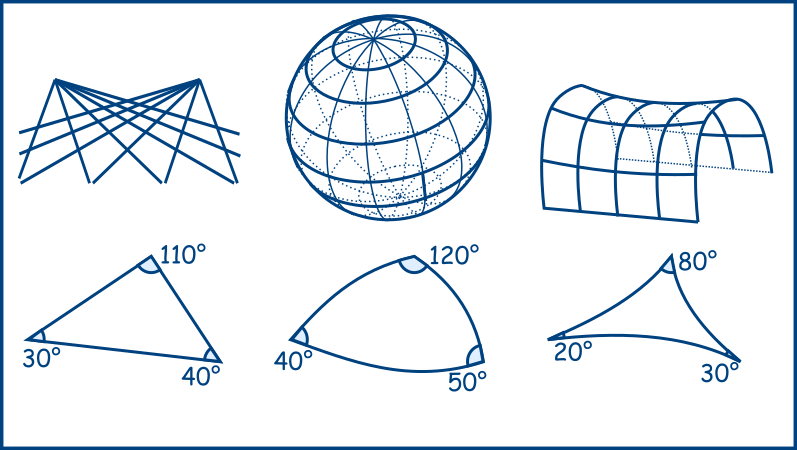
Was Euclidian wrong then? Only for triangles outside a 2D plane.
It means a truth depends on its environment or context (in math axioms).
It means 2+2=4 can be true in one environment, while 2+2=11 is true in another.

A new postulate about truth

Our brain is excellent at differentiating between what is similar and what is different.

”Similar” does not even mean completely equal. Things can share similarities but can be completely different on other aspects. Math can help with that.

Math gives the ability to differentiate even more: i.e. something can be greater or lesser. The difference can even be measured in numbers.

You might get the illusion that the concepts or objects are true, but the truth-statement is only for the comparison and not for the compared.

What about facts?
A fact is true when the similarity between the language statement (fact) and the objective world is verifiable.

What about objectivity?
Something is objective when the measurements of it are verifiable.

What about verifiable?
Verifiable means something will give the same or similar result when measured.

What about ambiguity?
Similar does not mean equal. Something may be equal in a particular context, but might also be completely different in another context.

What it all means?
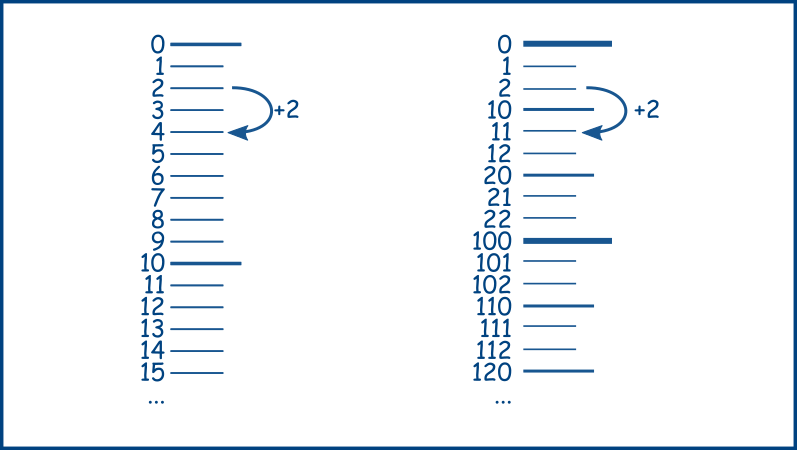
2+2=11 is false in decimal (base10: 0, 1, 2, 3, 4, 5, 6, 7, 8, 9,  10, 11, 12, … ).
2+2=11 is false in binary (base2: 0, 1,  10, 11, 100, 101, 110, 111, 1000, …)
2+2=11 is true in ternary (base3: 0, 1, 2,  10, 11, 12, 20, 21, 22, 100, …)

How to apply it?

It enables us to better understand logic, religion, science, math, philosophy and paradoxes.

Logic

When someone asks you, to tell the truth, what they mean is, that your language-statement must be similar to what happened in reality (i.e., the objective world).

The statement “It is raining outside” is the only truth, when it is raining outside. (Because the language statement can never be true, but the comparison can.

Religion

Religious truth is when there is a similarity in the subjective believe and the culturally accepted belief.

Science

Science is about comparing domain-specific datasets. Therefore a scientific truth is a similarity in the domain-specific datasets.

Math and philosophy are about comparing “comparison systems.” and therefore meta-sciences.

Examples of comparison systems:

1. 1. Boolean: True (Similar) or False (different).

1. 1. Operational: Greater than, Equal, Lesser than, etc.

1. 1. Numerical: How large is the difference.

1. 1. Geometrical / Multi-dimensional / Vectorial:  Size of difference in multiple attributes.

1. 1. Statistical: Correlation

1. Algorithmic: Similarity in input/output, computation, etc.

Paradoxes

There are at least three possible outcomes of a comparison:

1. 1. Similar (truth).

1. 1. Different (falsehood).

1. Not possible to compare (paradox).

The paradox: “This statement is false” is a paradox, since “something different from itself” is incomprehensible and cannot be compared to anything.

The paradox: “This statement is true” do not seem like a paradox, but it is, since comparing something to itself is as fruitful as not comparing; “How tall are you? I am as tall as myself.”

Gödel’s incompleteness theorem would be translated into: “There will always be something outside your comparison system and therefore cannot be compared.”

Comparison system	Outside of comparison system (paradox)
Natural numbers [1,2,3,…]	Negative number -1
Natural numbers can be expanded into Whole numbers […, -2, -1, 0, 1, 2, …]	Fraction: ½
Whole numbers can be expanded into Rational numbers […, -1, … , -½, …, 0, …, ½, …, 1, … ]	Irrational number: π
Rational numbers can be expanded into Real numbers: Rational and Irrational numbers	Imaginary number: square root of -1
Real numbers can be expanded into Complex numbers: Real and Imaginary numbers	Eternities: ∞
Etc.	Etc.

Artificial Intelligence

If truth is the relation of similarity between two or more objects, then current Machine Learning would be working with truths:

• Supervised Deep Learning would be fed with truthful data.
• Unsupervised Deep Learning would create its own truth from the data it’s fed with.

The fun fact

Testers are experts within detecting differences and similarities, so maybe I should change my professional title from “Test Engineer” to “The Truth Guru.”